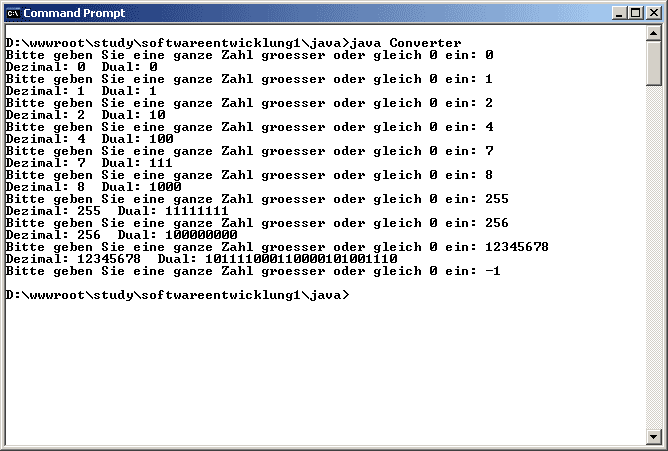
Die wohl an einfachsten in einem Algorithmus abzubildende Methode der Umrechnung einer Dezimalzahl in eine Dualzahl, ist die iterative Division durch 2, wobei der Rest dieser Division immer die nächste Dualzahl von links nach rechts darstellt. Als Abbruchkritierium wird die Eingabe einer negativen Zahl definiert.
Source
/**
*
* Softwareentwicklung I - Exercise 3/1.
* Convert positive integer number to binary number.
*
* @author Daniel Brunthaler (0255054)
* @version 1.0
*
*/
public class Converter {
/**
* Converts a given positive integer number into a binary number.
*
* @param number which should be converted.
* @return binary number in a String.
*/
public static String binary(long number) {
String binary = "";
do {
binary = number % 2 + binary;
number = number / 2;
} while (number > 0);
return binary;
}
public static void main(String[] args) {
String strInputPrompt =
"Bitte geben Sie eine ganze Zahl groesser oder gleich 0 ein: ";
long number;
IO.write(strInputPrompt);
number = IO.readLong();
while (number >= 0) {
IO.write("Dezimal: " + number);
IO.writeLn(" Dual: " + binary(number));
IO.write(strInputPrompt);
number = IO.readLong();
}
System.exit(0);
}
}
Die Grenzen ergeben sich durch den Datentyp long der Variable number. Es können
daher maximal Zahlen kleiner gleich 2^(64-1) eingeg. werden. Ein Sonderfall
ist die Eingabe eines nicht-numerischen Wertes. Dummerweise gibt die Methode
IO.readLong() in diesem Fall 0 zurück und liest keine neuen
Zahlen ein. Daher kommt es in diesem Sonderfall zu einer Endlosschleife. Da
auch die Dezimalzahl 0 umgerechnet werden können soll, könnte dieses
Problem nur durch das Entwerfen einer neuen Methode für das Einlesen von
long-Werten gelöst werden.
Eingabewerte: 0, 1, 2, 4, 7, 8, 255, 256, 12345678
Erwartete Ausgabe: 0, 1, 10, 100, 111, 1000, 11111111, 100000000, 101111000110000101001110
Zweck: Test, ob die Umrechnung richtig funktioniert.
Eingabewerte: -1
Erwartete Ausgabe: Abbruch des Prg.
Zweck: Test, ob die Beendigung des Prg. fkt.

Die Taylor-Reihe kann in einer do-Schleife berechnet werden, womit gewährleistet
ist, dass mind. ein Term zur Näherung ausgerechnet wird. Als Abbruchkritierium
dieser Schleife muss die Fehlerschranke berücksichtigt werden. Ist der
aktuelle Term kleiner oder gleich der Fehlerschranke, ist die Berechnung zu
Ende.
Die Fakultät wird in einer for-Schleife berechnet. Hierbei muss der Datentyp
double verwendet werden, da bei der Fakultät mit sehr großen Zahlen
gerechnet wird, der Datentyp long würde hierbei bald an seine Grenzen stoßen.
/**
*
* Softwareentwicklung I - Exercise 3/2.
* Approximatively calculation of exponantial function e^x.
*
* @author Daniel Brunthaler (0255054)
* @version 1.0
*
*/
public class ExponentialFunction {
public static int termcounter;
/**
* Calculates factorial of a given number.
*
* @param number of which factorial should be calculated.
* @return factorial.
*/
public static double factorial(double number) {
double factorial = 1;
for(double i = 2;i <= number;i++) {
factorial *= i;
// 1 * 2 first time, 2 * 3 second time, 6 * 4 third time ...
}
return factorial;
}
/**
* Calculates exponential function approxematively with Taylor.
* y(x) = e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + ...
*
* @param x power of e.
* @param errorBound error bound for Taylor.
* @return approxematively calculated exponential function with Taylor.
*/
public static double expTaylor(double x,double errorBound) {
double term;
double expTaylor = 1;
double i = 1;
do {
termcounter++;
term = Math.pow(x,i)/factorial(i);
expTaylor += term;
// 1 + x at the first time (1 + x^1/1!) then + x^2/2! ...
i++;
} while (term > errorBound);
return expTaylor;
}
public static void main(String[] args) {
String strStartPrompt = "Bitte geben Sie den Startpunkt ein : ";
String strEndPrompt = "Bitte geben Sie den Endpunkt ein : ";
String strIntervalPrompt = "Bitte geben Sie die Schrittweite ein : ";
String strErrorBoundPrompt = "Bitte geben Sie die Fehlerschranke ein : ";
String strTableHeader =
"Zeile x exp(x) Taylor exp(x) Java Fehler";
// column 0123456789012345678901234567890123456789012345678901234567890
// 0 10 20 30 40 50
double start, end, interval, errorBound, expTaylor, expJava, error;
int row = 1;
IO.write(strStartPrompt);
start = IO.readDouble();
IO.write(strEndPrompt);
end = IO.readDouble();
IO.write(strIntervalPrompt);
interval = IO.readDouble();
IO.write(strErrorBoundPrompt);
errorBound = IO.readDouble();
IO.writeLn(strTableHeader);
for(double x = start;x <= end;x += interval) {
expTaylor = expTaylor(x,errorBound);
expJava = Math.exp(x);
error = expJava - expTaylor;
IO.write(row + "",7);
IO.write(x + "",8);
IO.write(expTaylor + "",20);
IO.write(expJava + "",20);
IO.writeLn(error + "",20);
row++;
}
System.exit(0);
}
}
Da fast ausschließlich der Datentyp double verwendet wird, kann mit sehr großen Zahlen gerechnet werden. Die Grenzen des Typs double sind im Normalfall vernachlässigbar. Ein Sonderfall ist wiederum die Eingabe von nicht-numerischen Werten. Hierbei ergibt sich wieder dasselbe Problem wie in Aufgabe 1, da in diesem Fall die Methode IO.readDouble() den Wert 0.0 zurückgibt, aber keine neuen Zahlen mehr einliest.
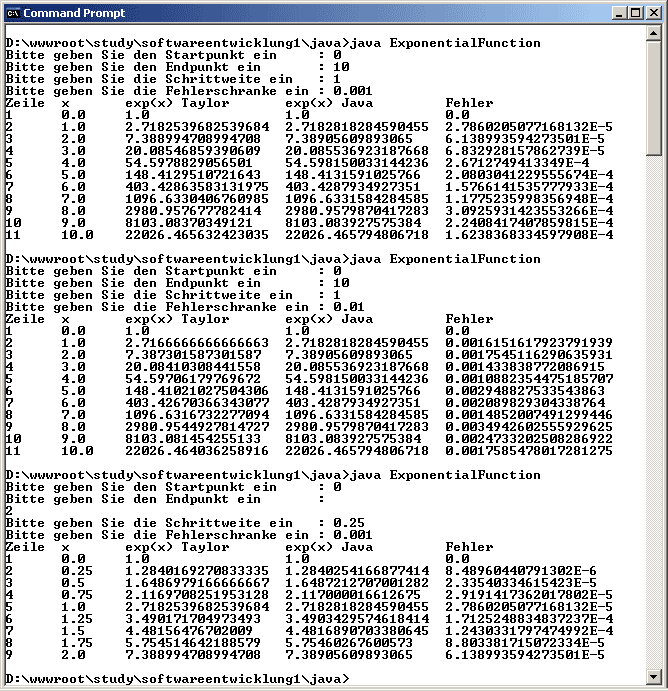
Eingabe: Startpunkt=0, Endpunkt=10, Schrittweite=1, Fehlerschranke=0.001
Erwartete Ausgabe: Gleiche wie in der Angabe
Zweck: Test, ob die Berechnung der versch. Werte fkt.
Eingabe: Startpunkt=0, Endpunkt=10, Schrittweit=1, Fehlerschranke=0.01
Erwartete Ausgabe: Berechnete Werte
Zweck: Test, ob Prg. richtig fkt., diesmal mit anderer Fehlerschranke
Eingabe: Startpunkt=0, Endpunkt=2, Schrittweit=0.25, Fehlerschranke=0.001
Erwartete Ausgabe: Berechnete Werte
Zweck: Test, ob Prg. richtig fkt., diesmal mit anderem Endpunkt und anderer
Schrittweite